A 4-Note Swiss Army Knife For Improvisers

Originating from a set of well known piano voicings, these structures form a quartet of unique 4-note “scales”. Due in large part to the presence of the intervals of a minor 2nd and tritone, they offer a good deal of “bite”.
This harmonic and melodic tension was first fully appreciated by such innovators as Joe Henderson, Woody Shaw, Herbie Hancock, McCoy Tyner, et al in the early 1960s and beyond.
Ex.1 – The 4 basic structures / inversions and their shared chord types.
1) Eb13 – 3rd, 6th (13th), 7th, 9th. As no 11th is present here, this combination works melodically with both natural and #11 - implying Mixolydian or Lydian Dominant colors, respectively.
2) Db Maj7#11 – Root, 3rd, 7th, #11. Implies a Lydian or Lydian Augmented sound.
3) Bb min6/9 – b3rd, 5th. 6th, 9th. Ascending Melodic Minor, as well as Dorian, are the implied colors.
4) A7alt – 3rd, b7th, #9th, b13th. A sub-set of the Altered Scale (7th mode of Melodic Minor).
5) G min7b5 – Root, b5th, b7th,11th, (no 3rd). Implies a Locrian as well a Locrian #2 sound.
The goal of this book is to present these voicings as a horizontal melodic (i.e. scalar) concept, with the single-line instrumentalist in mind. The introductory exercises and sequences - in 12 keys - found in the first chapter are designed to develop technical facility as well as aural familiarity with the shapes and sounds of the Super 4 tetratonic.
Take a close look at Ex. 2
Ex. 2 – The 4 basic structures – mutually exclusive – horizontally from a common tone C.
A set of four, unique tetratonic structures is generated - as it is from each step of the chromatic scale. Again, the 5 basic chord types are listed above each grouping.
Underneath, in the spaces between the notes - 1+4+2(+5), 2+5+1(+4), 4+2+5(+1) & 5+1+4(+2) – are numbers that signify the amount of semitones between each note (e.g. C – Db = 1 semitone; Db – F = 4 semitones; F – G = 2 semitones; G – C (octave) = 5 semitones. Hence, 1+4+2(+5).
The number in parenthesis is the number of semitones from the fourth tone in the group to the octave (i.e. G – C = +5 semitones)
This method of labeling is for the sole purpose of distinguishing one structure from the other. Notice that the numbers cycle around and that their order is constant (5 follows 2, 4 follows 1, etc.) regardless of structure.
The interval make-up of each structure from Ex. 2 (within one octave, C – C) looks like:
1+4+2(+5)
1 minor 2nd, 1 Major 2nd, 1 Major 3rd, 2 Perfect 4ths, 2 Perfect 5ths, 1 tritone, 1 Maj 7th
2+5+1(+4)
1 minor 2nd, 1 Major 2nd, 1 Major 3rd, 2 Perfect 4ths, 1 Perfect 5th , 1 tritone, 1 min 6th, 1 min 7th
4+2+5(+1)
1 minor 2nd, 1 Major 2nd, 1 Major 3rd, 1 Perfect 4ths, 1 Perfect 5th , 1 tritone, 1 min 6th, 1 Maj 7th
5+1+4(+2)
1 minor 2nd, 1 Major 2nd, 1 Major 3rd, 2 Perfect 4ths, 1 Perfect 5th , 1 tritone, 1 min 7th
The similarities between structures shouldn't be too surprising. After all, they are inversions of each other.
If we combine the interval possibilities (including the octave) from all 4 structures, we have ten of the twelve possible intervals at hand. The two missing intervals are the min 3rd and the Maj 6th – a tritone relationship.
The descending / ascending sequences in Ex. 3 give a different look at the Super 4 structures from a common tone, and are similar in concept to the X-Centric Pentatonic sequences found in the first few pages of “SUPER! Slick Licks That Stick!”
Ex. 3 – X-Centric Super 4 sequences from a common tone.
Ex. 4 – Connecting 514 to 425 - Cycle of 5ths
Ex. 5 – Perfect 4th / Tritone Combination
Ex. 6 – Super 4 minor ii-V7-i in Bb.
In Ex. 7 below, it seems that the ii7b5 / V7alt will once again resolve to a minor chord as in the previous example - but instead resolves to a Maj7#11 in measure #3.
Ex. 7 – Super 4 ii-V7alt resolving to Bb Maj 7#11.
Ex. 8 – Super 4 ii-V7alt resolving to a tonic dominant (Bb13).
Because of the tritone relationship between the two dominant chords (C7alt & Gb7#11) – which, in this case, are both part of the same C# (Db) Melodic Minor scale – they're really both the same chord with different notes in the bass (C and Gb, respectively).
Resolving to a tonic minor chord, this cadence is often found in bars #9 – 12 of a minor blues.
Ex. 9 – Super 4 bVI7-V7alt resolving to a tonic minor
“Blues in Super-4” is a 12-bar, two chorus etude, utilizing the 5 chord types previously discussed.
Both etudes are presented in Bb, Eb and Concert keys.
Creating meaningful musical lines with fewer note choices can be fun, challenging and rewarding - especially with an all-purpose tool like “The Super 4”.
B. Stern






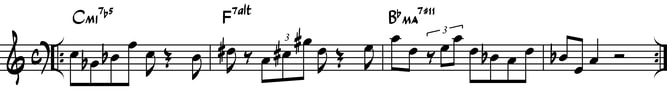







 RSS Feed
RSS Feed









