Twenty-four roads to Rome

It's the point from which you can embark on a short musical journey via 24 different routes.
Talk about variation!
For me, this particular concept of musical permutations was introduced initially via a book entitled "Inside Improvisation, Vol. 1 - Melodic Structures", by renowned tenor saxophonist and educator Jerry Bergonzi, which was published in 1994 by Advance Music.
This volume, as well as the other five belonging to the Bergonzi "Inside Improvisation" series, should be a part of the library of anyone who is sincerely interested in becoming a better improviser.
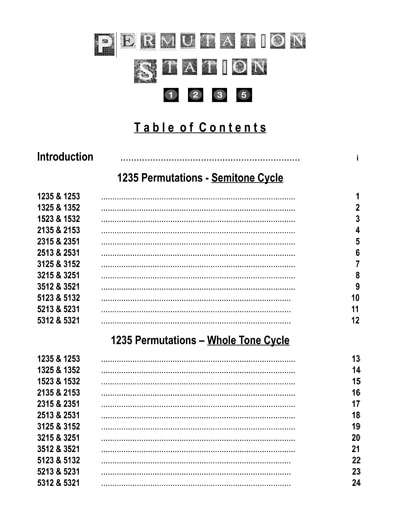
This month's Shortbook™, "Permutation Station - 1235", focuses on some of the concepts originally presented in "Melodic Structures" - specifically, the practical usage of the 24 permutations of Major scale steps 1, 2, 3 & 5 as an improvisational tool - while presenting it in the style of a Thesaurus or reference book.
So, why only four and not five note permutations?
Mathematically speaking, any group of 4 unique items yields 24 mutually exclusive arrangements of those same 4 items. In other words, 4 notes yields 24 unique permutations, while the 5 note Pentatonic Scale produces 120 permutations of 5 notes each.
While 24 is already a challenge for the average non-android to handle with ease, imagine having to deal with 120! Add to that the fact that, as the vast majority of Western music is in 4/4 time, phrases built with groups of 4 notes fit more naturally and evenly in a 4/4 measure than groups of 5.
That being said, if we were to order the numbers 1,2,3 & 5 as permutations, we would get the following 24 different groupings of those four numbers:
{1,2,3,5} {1,2,5,3} {1,3,2,5} {1,3,5,2} {1,5,2,3} {1,5,3,2}
{2,1,3,5} {2,1,5,3} {2,3,1,5} {2,3,5,1} {2,5,1,3} {2,5,3,1}
{3,1,2,5} {3,1,5,2} {3,2,1,5} {3,2,5,1} {3,5,1,2} {3,5,2,1}
{5,1,2,3} {5,1,3,2} {5,2,1,3} {5,2,3,1} {5,3,1,2} {5,3,2,1}
If we take the above numbers and translate them to the first, second, third & fifth steps of the Major Scale - in this case C Major - we get:
{C,D,E,G} {C,D,G,E} {C,E,D,G} {C,E,G,D} {C,G,D,E} {C,G,E,D}
{D,C,E,G} {D,C,G,E} {D,E,C,G} {D,E,G,C} {D,G,C,E} {D,G,E,C}
{E,C,D,G} {E,C,G,D} {E,D,C,G} {E,D,G,C} {E,G,C,D} {E,G,D,C}
{G,C,D,E} {G,C,E,D} {G,D,C,E} {G,D,E,C} {G,E,C,D} {G,E,D,C}
the first 2 lines of which (in bold) would look like this when notated:
The 1235 tetrachord yields two Major 2nds (C-D & D-E), one minor 3rd (E-G), one Major 3rd (C-E), one Perfect 4th (D-G) and one Perfect 5th (C-G).
"Permutation Station - 1235" is organized according to the interval distance between each of the parallel 4 note permutation groupings - spaced in min & Maj 2nds & 3rds, as well as Perfect 4ths & 5ths).
Because of the extreme tonal nature of the 1235 tetrachord, it makes for a much more interesting and musical practice experience to play its permutations in ascending or descending fashion in half steps (Semitone Cycle), whole steps (Whole Tone Cycle), minor 3rds (Diminished Cycle), Major 3rds (Augmented Cycle), and the Cycle of Fourths (5ths), than if one would simply play them in one key, as in the graphic above; which would be monotonous and boring.
Working each permutation through all of the above mentioned cycles also familiarizes one with the different possible melodic & harmonic connection and resolution points between them, as it would with an actual tune.
The graphic below shows a 2135 permutation ascending in half steps (semitone cycle). It then descends as its retrograde (backwards - 5312).
How 'bout a 3251 permutation ascending in minor 3rds (Diminished Cycle), as well as its descending retrograde 1523. The Diminished Cycle splits the octave into to 4 equal parts, right?
Hence, the a, b, c & d designations.
Below is an example of a ii-V7-I in C Maj. built exclusively from 4-note permutations of 1235 from different key centers (shown under the chord symbols). Notice how they combine to provide chord tones, including alterations, for each chord quality and type.
These inversions, of which there are 4 for each of the 24 four note permutations (96 variations in total), are shown here for reference - in C only.
The below graphic shows a 1235 (CDEG) and a 1253 (CDGE) permutation, as well as their retrogrades (5321 and 3521) in all four inversions. They're ordered according to the lowest note in each 4-note group while ascending (CDEG, CDEG, CDEG, CDEG), and the highest note while descending (GEDC, GEDC, GEDC, GEDC ).
Using the sequences in this book as a reference, it is suggested to play through them and take note of the one's that you like.
There's a lot to like.
B. Stern












 RSS Feed
RSS Feed









